数据驱动商业决策之模型魅力(一):线性回归
在商业领域,各个行业、企业或组织都遇到前所未有的全球化、区域化或细分市场多元化的挑战,他们在激烈竞争中对生存和成长的需求推动了对大数据发展的探索和研究。有效地处理、分析和应用这些大数据解决商业问题、助力商业决策,已成为当今各个商业领域的迫切需求。笔者以易于接受的案例阐述、解释和演示商业分析涉及的数据模型(回归、分类、聚类、决策树、关联分析等等),探讨如何用技术和方法去解决实际商业问题。
前言
您可能需要估算企业的盈利能力,尽可能算出产品制造的最优成本,估计销售额的增长,估算公司的员工流失,决定未来可能的费用支出。在上述所有情况下,您需要了解这些因素与影响、决定或对它们造成冲击的其他因素的关联和关系,这里可能就存在一定的线性或非线性关系,从而引导商业决策。
线性回归是一种非常简洁而又强大的方法,描述自变量(响应变量)与因变量(目标变量)之间的关系,这意味着可以根据自变量的值来预测因变量的值。有一个自变量存在的回归被称为简单回归。当有多个自变量时,回归被称为多元回归。在线性回归的情况下,自变量与因变量之间的关系通过一条直线来解释,在非线性关系的情况下,自变量和因变量之间的关系是非线性的(多项式回归,如二次多项式回归、三次多项式回归)。本文所介绍的线性回归,在整个机器学习家族的关系如下图所示:
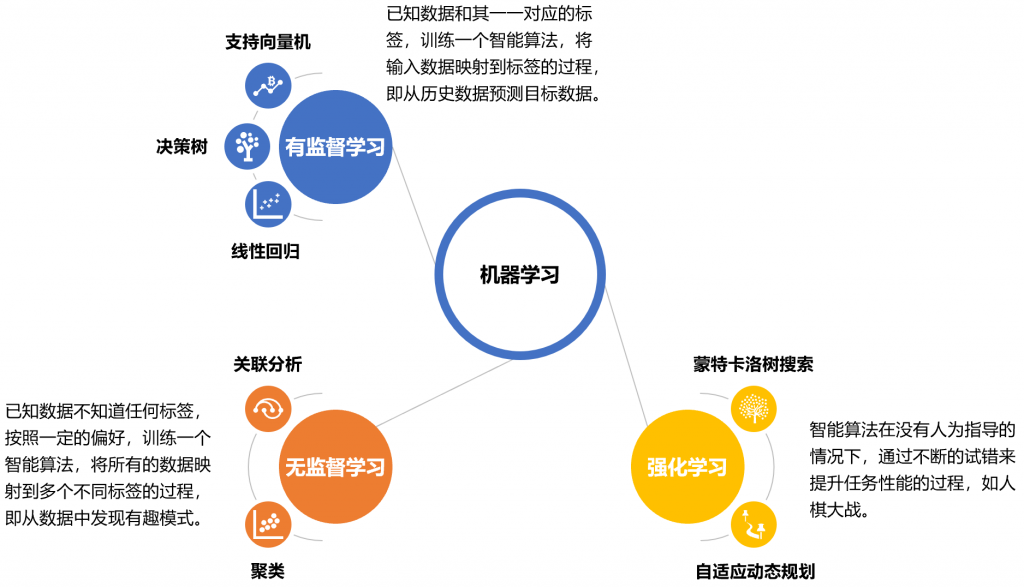
-300x300.png)
关注微信公众号,获取最新文章及下载资料
简单线性回归
正如前文所述,简单线性回归是指两个相关变量之间的线性关系:一个因变量和一个自变量。可以通过回归方程来描述:
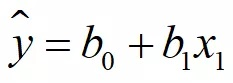
根据已知数据,计算出该回归方程线的截距(b0)、斜率(b1),从而预测目标值。实际上,回归方程线是一个平滑的平均数图形,它平滑每个自变量值的因变量的平均数,从而将拟合值的误差最小化。这种方法称为最小二乘法,它将自变量的实际值与自变量的预测值之间的平方差之和最小化。
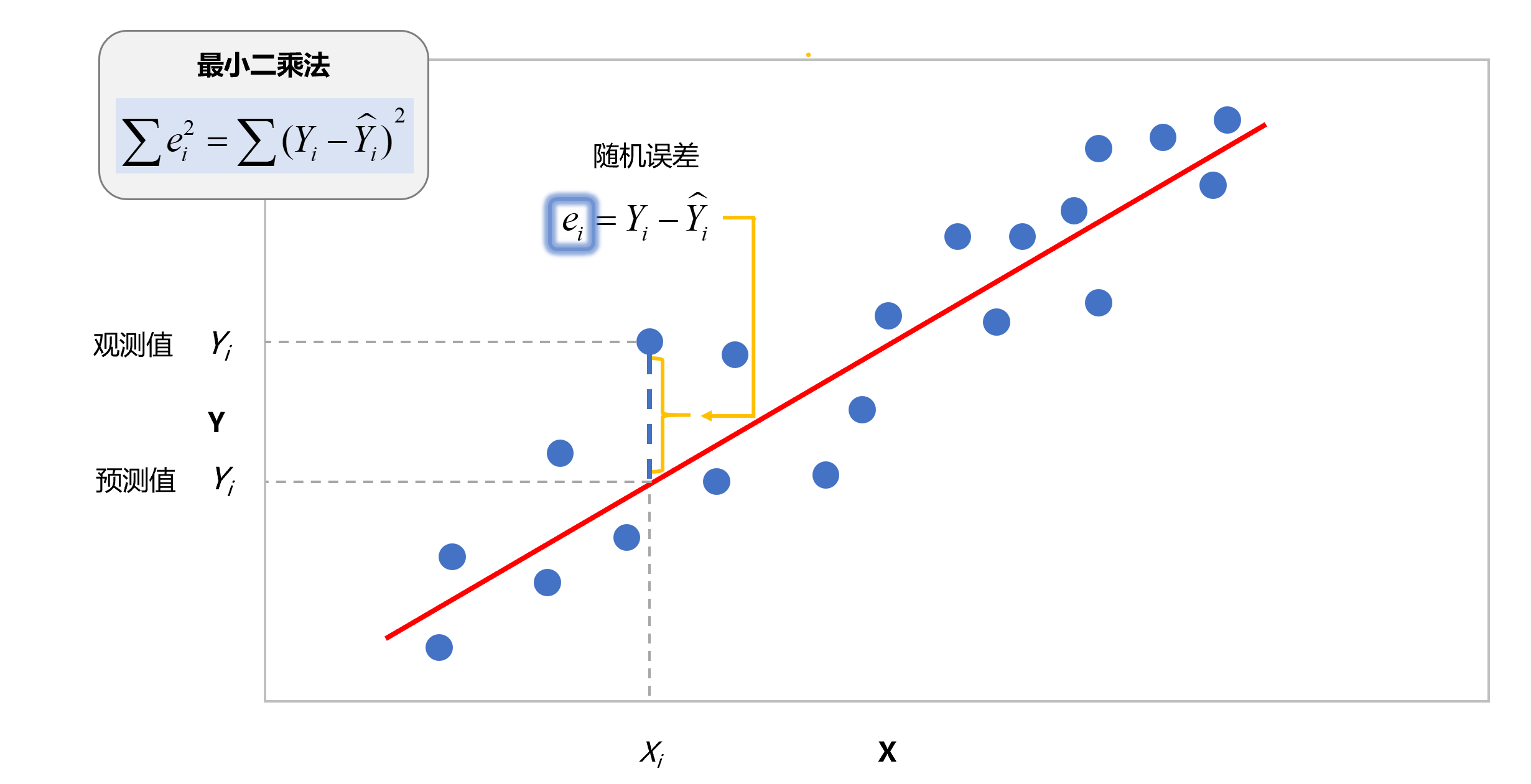
最小二乘线是使总体误差平方和最小的线,利用微积分方程求偏导,可以推算出:
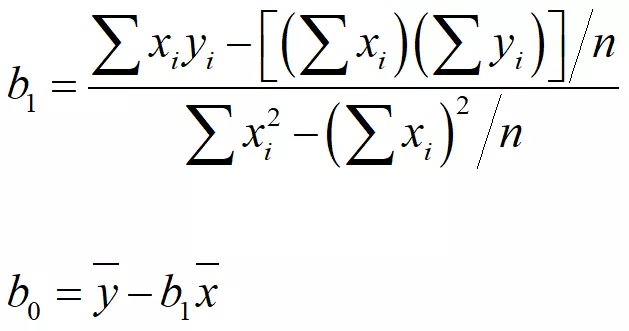
多元线性回归
与简单线性回归不同的是,多元线性回归是指多个相关变量之间的线性关系:一个因变量和多个自变量。可以通过回归方程来描述:
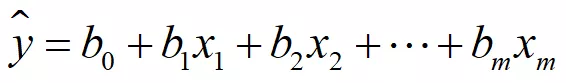
与简单线性回归一样,多元线性回归模型也是要求误差平方和为最小的前提下,用最小二乘法求解参数。但是,求解难度随着自变量的增多变的异常复杂(涉及概率论、矩阵论、偏微分方程),可以直接利用计算机工具进行求解,这里就不再详述。
建立多元线性回归模型时,为保证回归模型具有优良的解释能力和预测效果,应注意自变量的选择,其准则是:
(1)自变量对因变量必须有显著的影响,并呈密切的线性相关;
(2)自变量与因变量之间的线性相关必须是真实的,而不是形式上的;
(3)自变量之间应具有一定的互斥性,即自变量之间的相关程度不应高于自变量与因变量之间的相关程度;
(4)自变量应具有完整的统计数据,其预测值容易确定。
然而,在对一组数据进行分析时,并不知道自变量与因变量之间的关系,也不清楚其是否符合线性回归模型的典型特征,所以需要进行必要的检验与评价。该规则同时适应简单线性回归,具体如下:
(1)拟合优度,是指回归直线对观测值的拟合程度。度量拟合优度的统计量是可决系数(亦称确定系数)R²。R²最大值为1。R²的值越接近1,说明回归直线对观测值的拟合程度越好;反之,R²的值越小,说明回归直线对观测值的拟合程度越差。
(2)标准误差,是因变量的实际值与回归方程求出的估计值之间的标准误差,估计标准误差越小,回归方程拟合程度越好。
(3)回归方程的显著性检验,即检验整个回归方程的显著性,或者说评价所有自变量与因变量的线性关系是否密切。通常采用F检验,该检验对服从正态分布的数据非常敏感,应用非常广泛。根据给定的显著水平(比如置信水平95%)、自由度查F分布表,得到相应的临界值Fa,若F(回归方程)>Fa,则回归方程具有显著意义,回归效果显著;若F(回归方程)<Fa,则回归方程不具有显著意义,回归效果不显著。
(4)回归系数的显著性检验。在简单线性回归中,回归系数显著性检验(t检验)与回归方程的显著性检验(F检验)是等价的,但在多元回归中,这个等价不成立。t检验是分别检验回归模型中各个回归系数是否具有显著性,以使模型中只保留那些对因变量有显著影响的因素。根据给定的显著水平(比如置信水平95%)、自由度查t分布表,得到相应的临界值ta,若t(回归方程)>Fa,则回归系数具有显著关系;若t(回归方程)<ta,则回归系数不具有显著关系。
(5)多重共线性,是指自变量之间具有较强的线性关系,这种关系超过因变量与自变量的线性关系,则回归模型的稳定性受到破坏。需要指出的是,在多元回归模型中,多重共线性是难以避免的,只要不太严重就行了。判断多元线性回归方程是否存在严重的多重共线性,可分别计算每两个变量之间的可决系数r²,若r²>R²或接近R²,则应设法降低多重线性的影响。
案例
在房地产买卖市场,房价受住宅面积、房龄、地段等因素密切相关,定量预测房价对房地产业的商业分析决策具有一定的意义。本文根据从DASL(The Data And Story Library)官网下载的数据,描述的是纽约州某地房价的随机数据样本,维度如下:
本文用RStudio对该数据进行线性回归分析。RStudio是一款R语言的IDE,R自带的环境操作起来可能不是方便,而Rstudio很好地解决了这个问题,而且它还具有调试、可视化等功能,支持纯R脚本。RStudio可以在官网上下载试用,安装也非常方便,限于篇幅就不再赘述。
(1)导入数据
> houses<-read.table(“D:/houses.csv”,header = TRUE,sep = “,”)
- houses是定义的变量,在R语言中称之为数据框;
- <-read.table(“D:/houses.csv”,header = TRUE,sep = “,”),是导入数据文件(同时导入单元格标题),并赋值给houses;
- 可以通过> View(houses)查看数据。
(2)简单线性回归
构建房价(因变量)和住宅面积(自变量)之间的简单线性模型,代码如下:
> mod_simp_houses<-lm(Price~Size,data=houses)
> summary(mod_simp_houses)
- lim(因变量 ~ 自变量,数据=数据框名)是建立线性关系的命令;
- 可以通过> summary(mod_simp_houses),查看线性模型的计算结果。
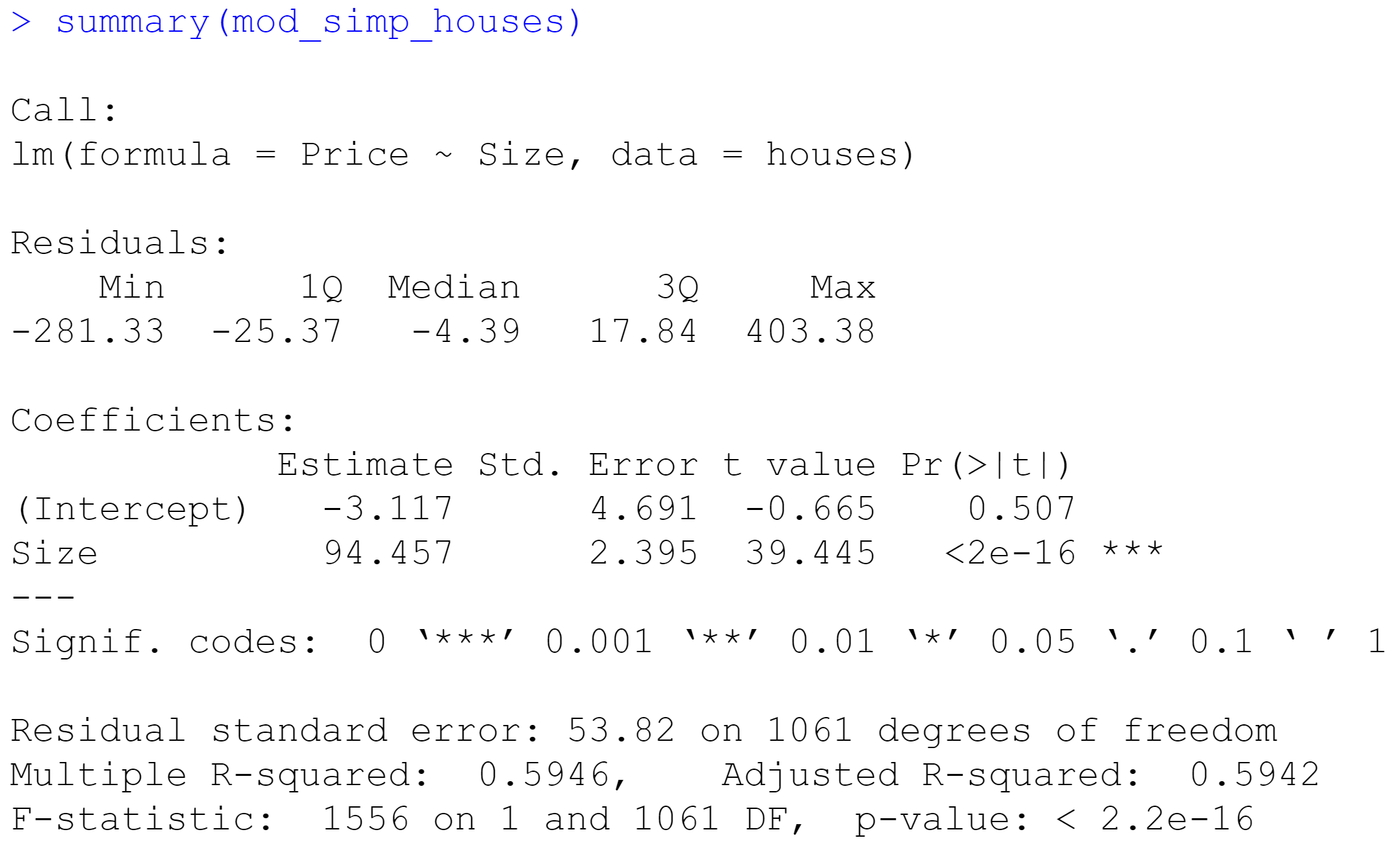
残差(Residuals)描述了因变量的实际值与使用回归方程预测的响应变量的值之间的差。最大残差403.38、最小残差-281.33,差异非常大,理想状态越小越好。另一方面,中位数(Median)-4.39,接近于0,说明还是符合回归方程减少差异的初衷,但是存在一定的差异点。
模型系数(Coefficients)给出默认置信水平(95%)下的进一步详细信息。这里的截距(b0)由截距估计值(the intercept estimate)(即-3.117)、斜率(b1)由Size估计值(即94.457)给出。因此,简单线性回归方程如下:
Price = -3.117 + 94.457 Size
多重R²(Multiple R-squared)是可决系数,调整后的R²(Adjusted R-squared)是调整后的R²调整值,避免过度拟合。调整后的R²是0.5942,远低于1,显示因变量与自变量之间并不良好的关系。F统计量(F-statistic)是基于F检验的,应越小越好(0.001、0.005、0.01、0.005),否则整个线性模型是不显著的。本例中,F统计量是1556,非常大。
也可以输入命令(> crPlots(mod_simp_houses),需要使用library(car)),获取组合残差图,如果红线与蓝线不重合且分离较大,可以直观得出简单线性模型拟合效果即线性效果不佳。如下图所示:
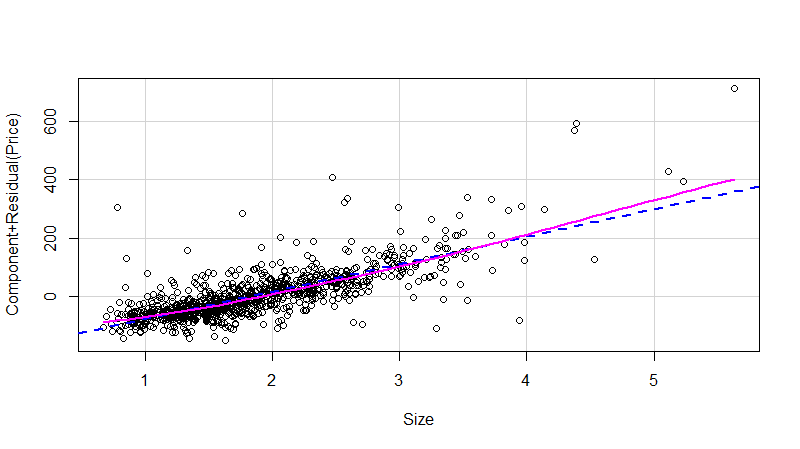
所以,整体上该简单线性回归模型不理想,价格(Price)与面积(Size)之间存在弱相关的线性关系,应引入其它变量因素,进一步验证多元线性回归模型。

可以看出,房价(Price)与住宅面积(Size)、浴室(Baths)、卧室(Bedrooms)、壁炉(Fireplace)相关性大一些,与土地面积(Acres)、房龄(Age)相关性非常弱。
第二,利用lm()函数构建房价(因变量)与住宅面积(自变量)、浴室(自变量)、卧室(自变量)、壁炉(自变量)之间的多元线性回归模型:
> mod_mult_houses<-lm(Price~Size+Baths+Bedrooms+Fireplace,data=houses)
第三,通过summary()函数,生成该多元线性模型的摘要信息。
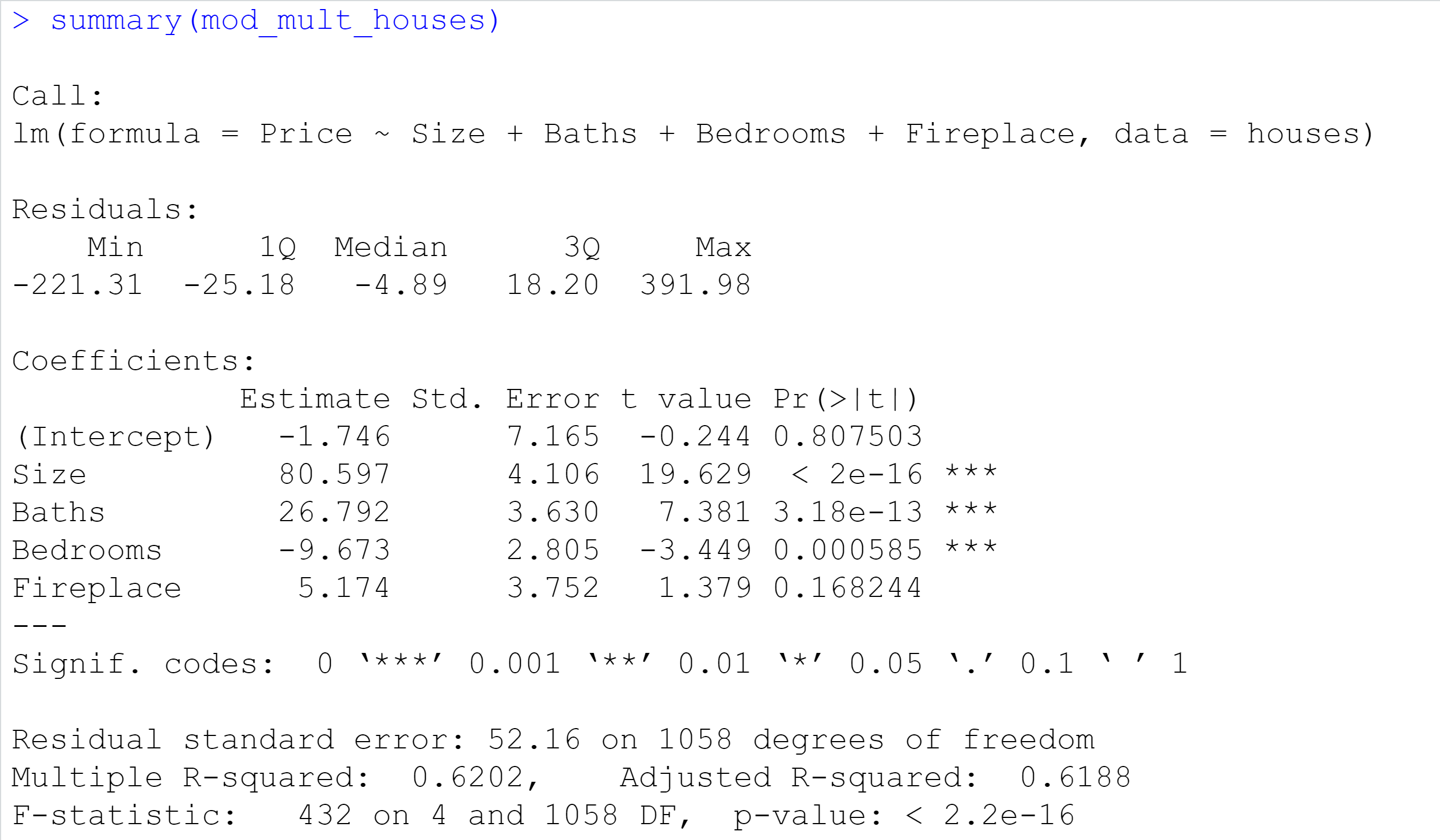
通过上述摘要,可以看出壁炉(Fireplace)的显著性水平不好(Pr(>|t|)),应从模型中去掉。所以,重新构建多元线性回归模型:
> mod_mult_houses<-lm(Price~Size+Baths+Bedrooms,data=houses)
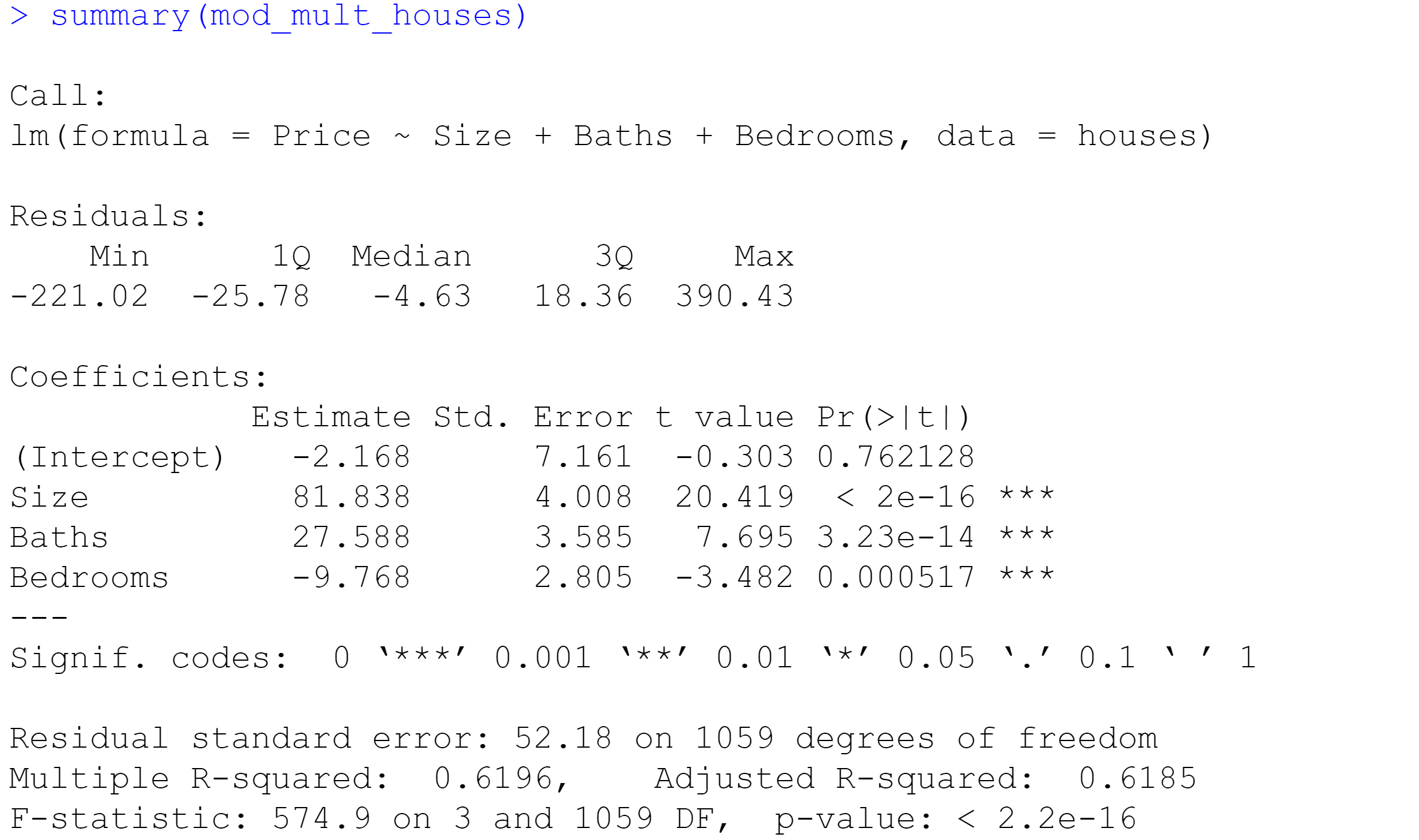
通过上述摘要(调整后模型),房价(Price)与住宅面积(Size)、浴室(Baths)、卧室(Bedrooms)的显著性水平较好,但是整体显著性水平还是较低的(0.762128>0.05)。此外,还可以看到调整后的R²(Adjusted R-squared)为0.6185,虽然低于1,但是比简单线性回归模型的调整后的R²(0.5942)高出一些。
第四,验证回归假设。在数据存在正态分布的前提下,可以采用较为简洁、快速的方法,使用qqPlot(模型名称,simulate=TRUE,envelope=0.95)(需要使用library(car))函数的可视化进行验证。
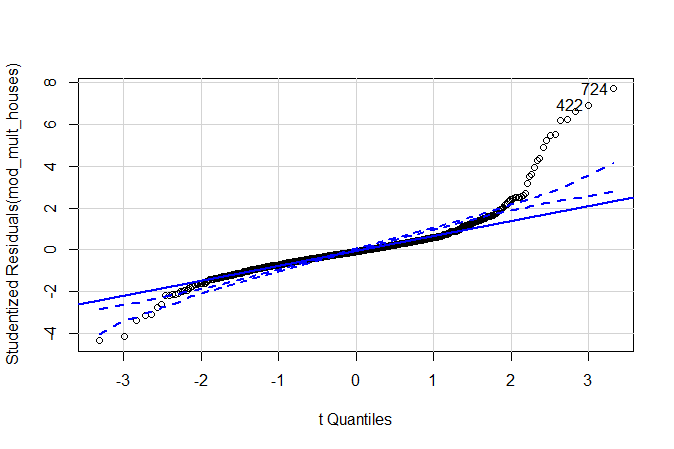
正如所见,有少量的点在置信区域之外。因此,可以假设残差是正态分布的,并且模型已经满足正态分布假设。
第五,验证多重共线性。使用vif(模型名称)可以很轻松地确定多重共线性。VIF代表方差膨胀因子,通常VIF值大于5,即存在严重的多重共线性,应该将影响变量剔除出模型。

可以看出,各自变量之间不存在严重的多重共线性。
最后,得出多元线性回归方程是:
Price = -2.168 + 81.838 Size + 27.588 Baths – 9.768 Bedrooms
——欢迎预约我们,现场沟通交流。
