深入浅出Excel VBA(四):随机多变量财务模型
VBA是Excel应用的高端技能,利用Excel灵活性的同时,极大增强数据处理能力,但是掌握起来有一定的难度。笔者基于真实的业务场景,从过往的从业、项目实施经验中凝练一些典型的VBA应用,希望对读者有所裨益。
场景
本文场景是基于随机多变量的多项资产投资组合模型的建模示例,该建模技术在其它众多场景中应用极为广泛,如果敏感性分析、成本规划、生产排序(后文会陆续介绍),也称为蒙特卡洛模拟。需要说明的是,关于本文提及的专业知识,在上篇文章《深入浅出Excel VBA(三):线性单变量财务模型》详细提到财务模型的定义,具体解释两项资产投资组合模型的概念(投资期望报酬率、方差、风险分散化效益)、建模示例等,这里就不再赘述。
多项资产投资组合的期望收益率和方差计算公式如下:

当相关系数低于1时,投资组合具有风险分散效应,但是如何发现有效的机会集,则需要建立该投资组合模型,揭示投资收益率与方差的关系,如下图:
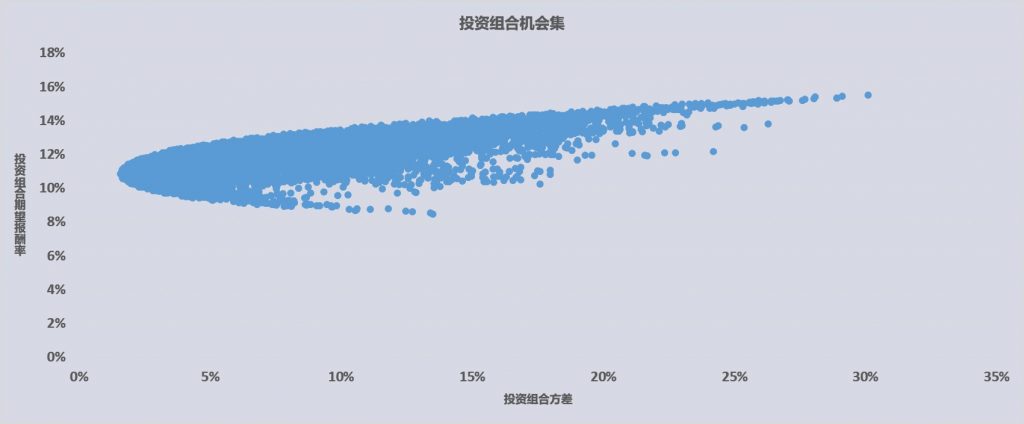
该图中,是以5项资产投资组合为参考建立的投资收益率、方差模型。可以直观看出,散点图的上边缘是具有风险最低、收益最高的有效曲线,即最佳投资组合。
-300x300.png)
关注微信公众号,获取最新文章及下载资料
技术解码
如果按照线性建模思维(具体参见《深入浅出Excel VBA(三):线性单变量财务模型》),构建前述的5项资产投资组合,需要百亿(1005)次计算,这是一个天文级数字,而且每向投资组合增加一项资产,计算量都是百倍的增长,对系统资源的损耗、时间的等待可想而知。
本文介绍的随机多变量是基于蒙特卡洛模拟方法,生成一定数量的随机数,这些随机数可以被控制服从相应的概率分布,比如平均分布、泊松分布。在现实世界,有很多模型是难以通过数学进行求解的,而利用蒙特卡洛模拟方法,既节省了时间,又能迅速找到最逼近最优解的答案,甚至是通过不断迭代最终找到最优解。
所以,通过随机生成多项投资组合中的资产比例,计算投资组合的期望报酬率、方差,可以迅速得到投资组合的机会集。当然,可以根据求解的精度、时间、概率分布要求,增加随机数据的样本数量,上图中提到的5项投资组合是随机生成10000个数据的计算结果,处理速度非常快。
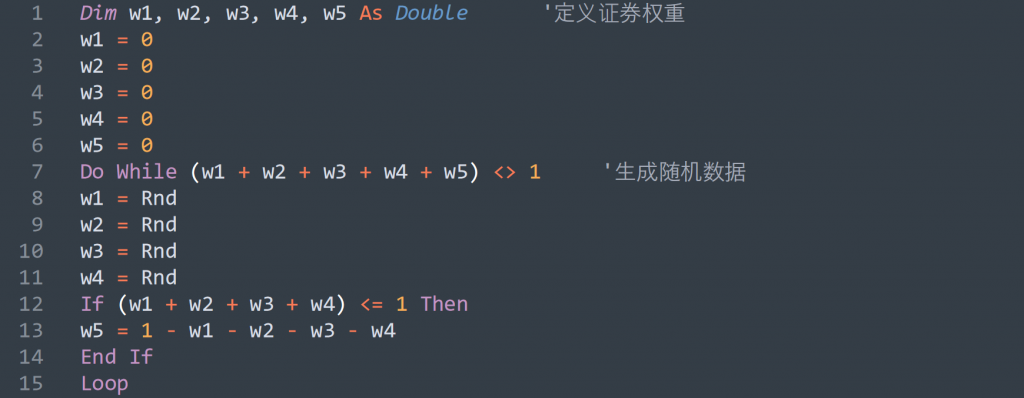
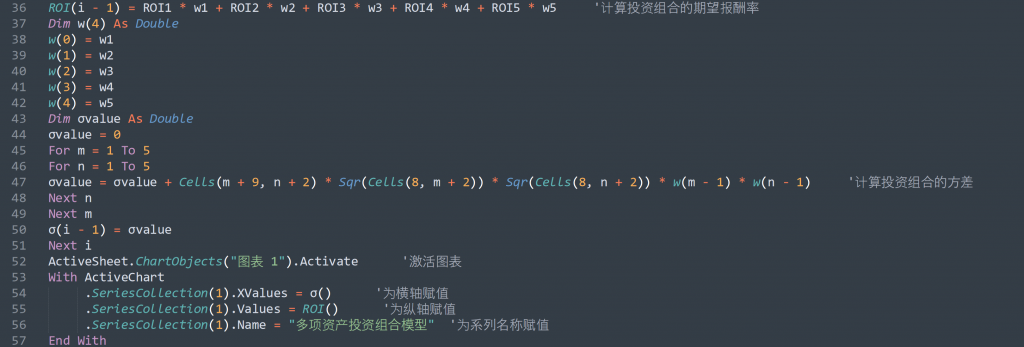
代码示例
——欢迎预约我们,现场沟通交流。
